~ Amplifier–Buffer PCB ~ ECC81–83 Graphs ~

Here is an enlarged section from the Mullard characteristic curve for an ECC81 taken from my BBC Wood Norton [Happy Days] training notes to support the Valve Amplifier/Buffer article ~ During the BBC transmission engineering courses we used these curves to calculate a.c. gains and d.c. operating points for various valve amplifier designs but not at currents as low as 1mA or anode voltages as low as 40V even with the sharpest pencil


Click image to see complete curve

There are 3 basic parameters that describe a Thermionic Valve ~ They can be read directly from or calculated from the manufacturers characteristic curves ~ In each case the parameter is calculated using 2 values while holding a third value fixed and this 3 dimensional approach to characterisation can be misleading unless you accept that in a practical amplifier the 'fixed' value will change and modify the parameter you used to make a calculation

µ ~ Is known as the amplification factor ~ It is the maximum gain a valve can achieve at a particular fixed anode current which in practice means using a constant current anode load and not loading the output ~ so a high input impedance follower may be required ~ The gain of the stage will vary with heater voltage and valve condition so some form of feedback will be required making a practical amplifier based on gain indicated by µ is impractical

From the graph above µ is calculated by measuring V_a between the points where the line I_a =1.1mA crosses the curves for V_g =0V and V_g ≈1V to give µ =∆V_a/∆V_g ~ this way µ gets calculated at 46 which I believe is lower than it actually is at this operating point ~ µ becomes greater as V_a lowers ~ For 1.1mA at V_a =200V µ =45 at V_a =170V µ =49 and at V_a =100V µ =52 ~ see other ECC81 curves below

g_m ~ Is known as the Mutual Conductance and is a measure of how much current a Valve will conduct for a given change in control voltage on one of its grids ~ Following the rules the parameter is determined with the anode and other grid voltages held constant so the maximum 'effect' of g_m can only be appreciated with a 0Ω or current mirror load or in practical amplifiers a transformer or inductor load

From the graph above g_m is derived by measuring I_a where the line 40V crosses the curves for V_g =0V and V_g ≈1V to give g_m =∆I_a/∆V_g (mA/V) ~ As you can see from the above curves the g_m at V_a =40V looks about 2.6mA for a 1V change in V_g but it is not 2.6mA/V in the region of the operating point due to the asymmetric ~ distortion producing ~ spread along the curve

r_a ~ Is known as the Anode Slope Resistance or the effective output resistance of a valve ~ It appears as a resistance in series with a voltage source inside the valve or across a current source inside the valve depending on the model used ~ r_a is measured with the grid voltages held constant and may appear of no use until you want to make a perfect current sink or output dependant distortion becomes a problem

From the graph above r_a is µ/g_m =∆V_a/∆V_g/∆I_a/∆V_g where the two ∆V_g cancel and r_a =∆V_a/∆I_a ~ But the values for µ and g_m derived from the curve above ~ around the point V_a =40V are not the most accurate ~ When trying to measure how an ECC81 and other valves performed in the Amplifier/Buffer circuit at low V_a and I_a I found myself plotting my own curves using a Tektronix 576 Curve Tracer [see below]

The complex interdependencies changing internal gains and impedances within a triode amplifier as V_a I_a and V_g change dynamically cause all kinds of distortion and colouration ~ Simply isolating one cause of distortion such as the non linearity of the I_a/V_g transfer function cannot fully explain the differences between the sound of similar or even the same type of valves

Some valve manufacturers publish other 'typical' curves that plot V_g r_a g_m and µ against I_a for a given V_a and these can be very useful working at low I_a but if the characteristics do not cover the V_a you are operating at then interpolation or guesswork is again required

It is likely that r_a is not measured independently and like the other parameters the results are adjusted to produce smooth regular curves ~ It should also be obvious when looking at valve characteristic curves that the specifications published for many valve amplifier 'designs' are also just 'typical' although many sound better than the design would suggest

Mullard ECC81 parameters µ gm r_a V_g plotted at V_a= 100V

Mullard ECC81 parameters µ gm r_a V_g plotted at V_a= 170V

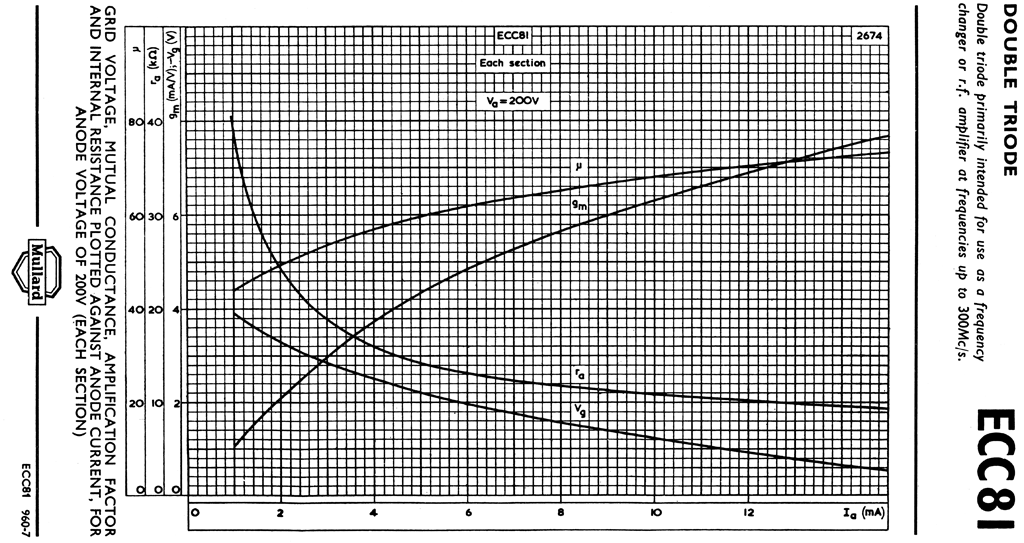
Mullard ECC81 parameters µ gm r_a V_g plotted at V_a= 200V

Mullard ECC81 parameters µ gm r_a V_g plotted at V_a= 250V

~ Plotting Characteristic curves using Tektronix 576 Curve Tracer ~

With an expanded scale and 0.5V steps in –V_g this area of the curves now looks more linear than the Mullard curves shown at the top of this page but the parameters µ g_m and r_a still vary greatly across this reduced area and It should be clear that a slight deviation from an optimum operating point will give less than optimum results and the distortion will change with signal level and d.c. conditions and changes in the heater voltage

This screen shot is the same ECC81 as above but now with a 27kΩ resistor in the cathode

As I mention in the Valve amplifier/buffer and LEAK amplifier gain reduction articles the modified g_m' of a valve with an un–bypassed cathode resistor R_k is reduced to about 1/R_k which in this case is about 35µA/V depending on the g_m of the valve

The anode voltage V_a sweeps to 200V as before but the anode current I_a range is now only 1mA and the –V_g steps are 2V with each step increasing I_a by about 70µA consistent with a g_m' of 35µA/V ~ Anode current does not start to flow until V_a > –V_g as seen

The curve looked like a flat line at the bottom of the display until the x scale was made 100µA/div but even then did not look suitable for use as an amplifier because in practice the 27kΩ resistor 'self biased' the valve to almost 'cut off' unless the grid is raised +ve ~ Using the TEK–576 the effect of the grid being made +ve can be simulated using the step offset control which can be set to a maximum of ±10x the step voltage ~ here the steps are 2V allowing a +20V offset

This characteristic looks more like a pentode or even a transistor due to the increase in r_a to >1.2MΩ ~ The ∆I_a between V_g steps is very linear and additional steps above and below those shown will run virtually parallel making interpolation and parameter measurements very easy ~ A load line can be drawn on the curve referenced from 0V as R_k is now part of the active device

The load–line for an anode load of 100kΩ [used in the Amplifier/Buffer article] and a 180V supply is drawn onto the curve in the usual way between the points I_a =0V when V_a =180V and V_a =0V when I_a =180V/100kΩ =1.8mA ~ Unlike normal triode curves the position of the load–line along the V_a axis is not so critical for a.c. amplification due to the regular spacing and slope of the V_g steps

Using this [used old] ECC81 the amplifier gain calculated where the load-line crosses V_g=2V and V_g=20V is about V_a =58V/V_g =18V giving a gain of 3.22x [100kΩ/27kΩ =3.7x] ~ Due to the regular spacing of the V_g steps the operating point can be positioned almost anywhere along the load–line without a change of gain so an optimum point can be

An un-bypassed cathode resistor has such a significant effect on the g_m of a triode that in the 10dB [3.16x] version of the amplifier/Buffer even an old ECC81 that had failed AVO testing with 20% g_m gave good results

Changing the ECC81 for an ECC82 which for the same operating conditions normally has lower g_m r_a and µ gives an amplifier gain of 9dB ~ If this substitute were done in a traditional design the results would be .  .  .

From the ECC82 curves with R_k =27kΩ shown on the left the g_m is again about 35µA/V but the slope of the V_g steps is steeper because r_a has only been increased to r_a'≈ 460kΩ ~ The gain calculated from the load–line is V_a =52V/V_g =18V =2.89x or 9.2dB which correlates well with g_mxR_a' and measured the results

Changing the ECC81 for an ECC83 which tends to have more than twice the r_a and µ but a lower g_m [and apparently is designed to work at low I_a] the amplifier gain is now 11dB ~ As before if this substitute were done in a traditional design the results would be unpredictable

From the ECC83 curves with R_k =27kΩ shown on the right the g_m is once again about 35µA/V but the slope of the V_g steps is less because r_a has been increased to r_a' ≈2.8MΩ

The gain calculated from the load–line is about V_a =64V/V_g =18V =3.55x or 11dB which correlates with the measured results and those of my un—bypassed Rk calculator

The Amplifier/Buffer project was not specifically 'designed' for an ECC83 or an ECC82 ~ The chosen operating point for the available HT of 180V and gain of 10dB was for an ECC81 which I tend to use a lot

As shown above an un–bypassed high value cathode resistor tends to lower but also 'normalise' the g_m and increase the r_a of the gain stage triode so we get predictable gain and operating point for a wide variety of different triode types simply plugged into the same circuit

Local negative feedback across a R_k of 27kΩ reduces the distortion from this simple amplifier and allows higher than normal input voltage before input overload ~ The gain is predictable and the reduction of capacitors in the signal path should make for a 'better sounding' gain stage

As the value of R_k is reduced the gain increases as does distortion until a point is reached where R_k [still un–bypassed] becomes the value of an auto bias resistor and any further reduction would require a negative grid supply or a bypass capacitor to increase gain and the ability to simply swap valve types would be lost

Using an ECC81 auto biased for a gain stage I_a ≈ 1mA due to R_k=1.8kΩ with R_L=100k a gain of 27dB with low distortion is possible but not as predictable as when set for lower gains with higher local feedback due to higher values of R_k ~ Whether auto bias or higher values of R_k are used a cathode follower buffer ensures the gain is not affected by loading

 

Manufacturers like Mullard RCA and Brimar published curves of V_g r_a g_m and µ against I_a [like those shown here and above] in addition to the more common I_a/V_a characteristics but only for limited values of V_a and I suspect with r_a calculated rather than measured

The Mullard curves for the ECC83 were only supplied for V_a=100V and V_a=250 and this along with published application circuits led to many similar [me too] ECC83 based 'designs' which could have been better optimised with a little effort and by investigating other operating conditions around a lower V_a

Using a valve tester like the AVO163 g_m can be measured reasonably accurately and directly while monitoring I_a at low V_a [provided the meters have been modified to read correctly or external meters are used] but either µ or r_a also need to be determined by some other means

 

With a valve tester or a Curve Tracer r_a can be determined from r_a = ∆V_a/∆I_a by switching the anode voltage steps but at low V_a r_a is often 10s of kΩ and determining the small change in I_a [due to a change in V_a alone] may be difficult

My un—bypassed Rk calculator does not use g_m to determine its results but does calculate µ from entered values for g_m and r_a ~ By using all 3 values taken from valve characteristics or measurements a check that µ = g_m x r_a should be made to confirm the values

If you have read this far and have been looking at the graphs of V_g r_a g_m and µ against I_a you may notice that these curves change more at low I_a which leads some to use higher I_a in an attempt to get lower distortion but good circuits like the QUAD 22 prove that high I_a is not always required

" Darling if you only knew ~ Half as much as everybody thinks you do "